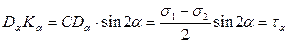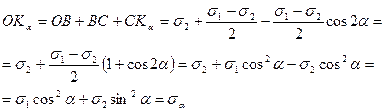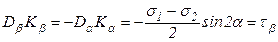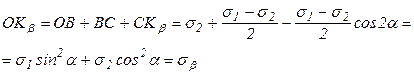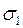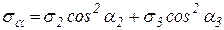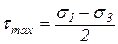Круги мора для главных напряжений

Круг мора и формулы

Круг мора

• Больше кругов Плоское напряженное состояние в определенной точке исследовалось аналитически. Вы также можете легко получить графическое представление, которое можно выразить аналитически до получения всех существующих формул. Для этого представим в качестве координат точки на плоскости XY TA. Чтобы узнать, каково

геометрическое расположение этих точек, используйте: Запишите константы a-St1— и R = -Да, 2 2 в формулах (3.14) и (3.15) Эти выражения принимают следующую форму: х-а + я cos2A; Грех 2А для у = R. (3,19) Уравнение (3.19) представляет собой круговое

уравнение, записанное в параметрической форме, центр которого находится на Людмила Фирмаль

оси o на расстоянии a от начала координат (рис. 89). Этот круг дает геометрическую интерпретацию задачи. Он называется кругом напряжений в честь предложенного немецким ученым Отто Мора или кругом Мора. х Рис 89А Соответствует ли произвольная область наклона, определяемая углом a на окружности, точкой? Мы будем

называть точки, нарисованные на этом сайте. Из уравнения (3.19) углы a и 4-90 ° на окружности напряжений соответствуют двум точкам K и Ri (см. Рисунок 89 в конце того же диаметра). Таким образом, для построения круга достаточно знать координаты этих точек: Od, TA и AA + EO °, TA + 90o == — TA> т.е. на любых двух участках,

• перпендикулярных друг другу. Затем, сосредоточив внимание на положении точки K и оси a-t, можно построить саму окружность напряжений на отрезке KKi, как диаметр. В этом случае вы можете сделать эти сайты. После этого круг родинок строится на точках 1 и 2, лежащих на оси а, как видно из рисунка. 89. 95, фиг. 90 указывает круг Крота, построенный с любым начальным местом и напряжением Тул. И ху-ху-ху ч. Его структура выглядит следующим образом: 1. Для осей

a-t отложить значения нормальных и тангенциальных напряжений в одном и том же масштабе и построить точки изображения в соответствии с координатами вертикальных координат l (a /, Tul) и горизонтальных / Людмила Фирмаль

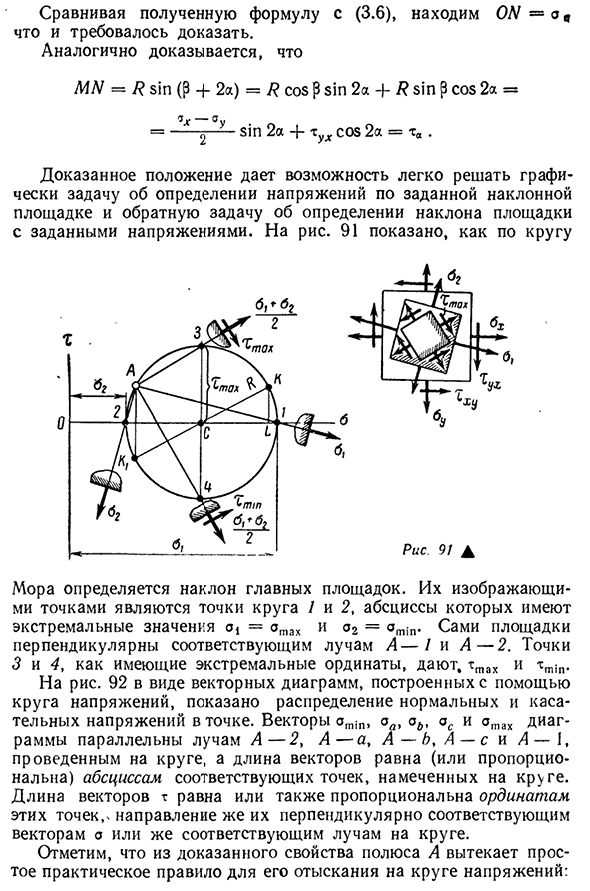
пересечении окружности и линии является точкой этого участка. Докажите заранее, отметим, что ник. = 2A, центрированный на той же дуге, что и вписанный ^ iM AK-a. = OS + CN = -i- + R cos (? + 2A) = ++ R cos p cos2A-sin p sin 2A. Но так как K, потому что p = CL = -x2—, R sin p = KL = tul_, то _Su-4-I — G V ON— —————— —— c s2A-Tuh Sin 2A. Если мы уравняем полученное уравнение с (3.6), то увидим, что существует CW = a a, который необходимо доказать. Аналогичным образом доказано, что MN-R sin (p4-2A) = R cos p sin2A + R sin p cos2A = sin2A + tuh cos2A = TA. Это позволяет легко графически решить проблему определения напряжения на данной наклонной платформе и обратную задачу

определения наклона площадки из-за данного напряжения. Для риса. 91 показан в виде круга Мора определяется наклоном основного сайта. Точки, которые они представляют, представляют собой круги 1 и 2, и их абсциссы имеют экстремальные значения с = atah и A2 = at! Сама платформа перпендикулярна соответствующим балкам А-1 и А-2. Точки 3 и 4, имеющие экстремальные координаты, ttah и nmin. Для риса. Распределение нормальных и касательных напряжений в точках показано в виде векторной диаграммы, построенной с помощью круга напряжений 92. Иллюстрации векторов amin, OA, GL, AC и amax параллельных лучей A-2, A-a, a- ■ B, A-C и A-1 находятся в круге, а длина вектора — в круге. И т.д. на горизонтальной оси

соответствующей точки Длина вектора t равна или пропорциональна продольной оси этих точек, а его направление перпендикулярно соответствующему вектору a или соответствующему лучу на окружности. Обратите внимание, что проверенные свойства бара означают простое практическое правило нахождения его в круге давления: 4 Заказ № 1037 97 Полюс А находится на пересечении лучей, перпендикулярных исходному участку соответствующей точки формирования изображения К. 90 Эти лучи обозначены пунктирными стрелками. Из круга напряжений нетрудно аналитически установить многие из ранее полученных зависимостей. Так, например (рис. 91), A112 = OS ± R = OS ± V C L2 + # A2 = Это соответствует формуле (3.13) или ^ gpahgp Это соответствует (3.16).

Изучу , оценю , оплатите , через 2-3 дня всё будет на «4» или «5» !

Откройте сайт на смартфоне, нажмите на кнопку «написать в чат» и чат в whatsapp запустится автоматически.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Круг Мора для объемного напряженного состояния

Обратная задача.

Прямая задача

Построение кругов Мора

Графический метод исследования напряженного состояния в точке.

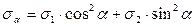
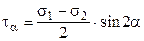
Можно оказать, что уравнения , представляют уравнение окружности в параметрической форме. Поэтому для графического метода исследования напряженного состояния используются круги напряжений, называемые кругами Мора .

В теории напряженного состояния можно разграничить две основные задачи:

Прямая задача:в точке известны положение главных площадок и соответствующие им главные напряжения, требуется определить нормальные и касательные напряжения по площадкам, наклоненным к главным под углом a.

Обратная задача: в точке известны нормальные и касательные напряжения, действующие по двум взаимно перпендикулярным площадкам, проходящим через данную точку, требуется определить главные напряжения и положение главных площадок.

Рассмотрим решение этих задач графическим методом

Аналитическое решение прямой задачи определяется формулами (4.6) – (4.9).

Для графического решения строится на плоскости в координатах s-t круг Мора

(рис. 4.9) в следующей последовательности.

Рис. 4.9

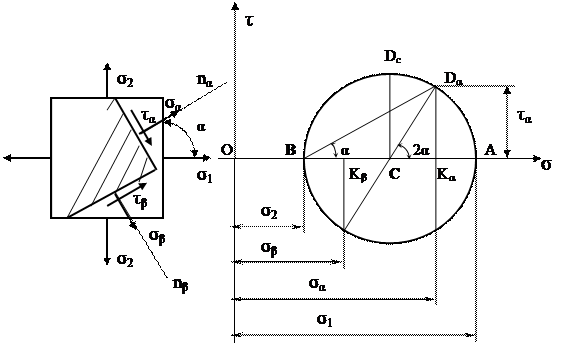Выбирается прямоугольная система координат так, чтобы ось абсцисс была параллельна большему из главных напряжений s₁, по этой оси в выбранном масштабе откладывются отрезки ОА и ОВ, численно равные напряжениям s₁ и s₂, а на их разности (на отрезке АВ) как на диаметре проводим окружность с центром в точке С.

Из крайней левой точки (В) круга проводим луч, параллельный внешней нормали к рассматриваемой площадке, т.е. под углом a к оси s. Точка пересечения этого луча с окружностью (D_a) имеет своими координатами отрезки D_aK_a и OK_a, численно равные касательному t_a и нормальному s_a напряжениям, действующим на рассматриваемой площадке.

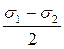
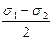
Из рис.4.9 следует: AC=BC=CD_α=, СК_α=СК_β =СD_αcos2α =cos2α

Точка D_b, лежащая на противоположном конце диаметра от точки D_a, характеризует напряжения s_β и t_b, действующие по наклонной площадке, перпендикулярной к первой.

Выполненные преобразования проведены с учетом, что 1+cos2α = 2cos 2 α., 1-cos2α = 2sin 2 α.

Полученные выражения для s_a, s_b, τ_α и τ_β полностью совпадают с аналитическими формулами (4.6) — (4.9).

В заключение следует отметить, что каждая точка круга Мора имеет своими координатами напряжения, действующие на соответствующей площадке, следовательно, зная главные напряжения для плоского напряженного состояния, можно с помощью круга Мора определить напряжения, действующие на различных площадках, проходящих через данную точку. Максимальное касательное напряжение соответствует точке D_c и равно радиусу круга.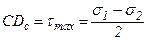

Довольно часто приходится решать обратную задачу, т. е. по напряжениям на произвольных площадках s_a, t_a, s_b, t_b определять величину и направление главных напряжений. Проще эта задача решается графически, т. е. с помощью круга Мора (рис. 4.10). Рассмотрим порядок его построения.

Прямоугольную систему координат s, t выберем так, чтобы ось абсцисс была параллельна большему из нормальных напряжений (пусть s_a > s_b). На оси s отложим в выбранном масштабе отрезки ОК_a, ОК_b, численно равные s_a и s_b. Из точек К_a и К_b проведем перпендикуляры К_aD_a, К_bD_b, которые численно равны соответственноt_a и τ_β (К_aD_a = t_a, К_bD_b = τ_β = — t_a). На отрезке D_aD_b, как на диаметре, построим круг с центром в точке С. Крайнюю правую точку пересечения круга с осью s обозначим буквой А, крайнюю левую – буквой В. Касательные напряжения в этих точках равны нулю, следовательно, ОА=s₁, ОВ=s₂ – главные напряжения (.в соответствии с прямой задачей).

параллельна большему из нормальных напряжений (пусть s_a > s_b). На оси s отложим в выбранном масштабе отрезки ОК_a, ОК_b, численно равные s_a и s_b. Из точек К_a и К_b проведем перпендикуляры К_aD_a, К_bD_b, которые численно равны соответственноt_a и τ_β (К_aD_a = t_a, К_bD_b = τ_β = — t_a). На отрезке D_aD_b, как на диаметре, построим круг с центром в точке С. Крайнюю правую точку пересечения круга с осью s обозначим буквой А, крайнюю левую – буквой В. Касательные напряжения в этих точках равны нулю, следовательно, ОА=s₁, ОВ=s₂ – главные напряжения (.в соответствии с прямой задачей).

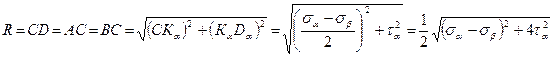
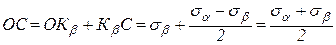
Из рис.6.10 определим радиус круга R и величину отрезка ОС (4.12)

(4.13)

C учетом выражений (4.12) , (4.13) получим следующие формулы для главных напряжений

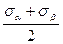
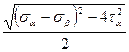
ОА= σ_I = ОС + R = + (4.14)

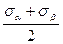
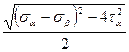
ОВ = σ_II = ОС – R = — (4.15)

Или 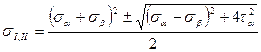(4.16)

Для определения направления главного напряжения s₁ проведем луч через крайнюю левую точку круга В и точку D_a¢, которая симметрична точке D_a относительно оси s. Направление луча ВD_a¢ совпадает с направлением s₁, направление s₂ перпендикулярно ему. Угол a₀ определится из треугольника ВК_aD_a¢ (рис. 6.10):

(4.17)

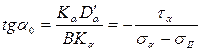
Угол a₀ считается положительным, если его откладывают от оси s против часовой стрелки.

4.7 Напряжения на произвольной площадке при объемном напряженном состоянии

В элементарном параллелепипеде, по граням которого действуют все три главных напряжения, рассмотрим произвольную площадку a, нормаль к которой составляет с координатными осями 1,2,3 углы α₁ α₂ α₃.(рис. 4. 11). На этой площадке будет действовать полное напряжение р_α, составляющее с нормалью n угол α. Определим его проекции на нормаль к площадке — σ_α и на саму площадку – τ_α.

Рис.4.11

Нормальное напряжение, исполь-зуя принцип суперпозиции, можно пред-ставить выражением =,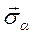

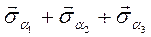
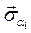
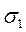
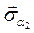
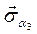
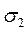
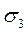
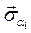
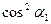
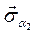
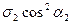
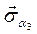
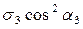
где— напряжение на рассматриваемой площадке, вызванное действием , а ,— соответственно от напряжений и.Для вычисления этих величин воспользуемся формулой для линейного напряжённого состояния: =, =, =.

С учетом этих значений нормальные напряжения на произвольной площадке определятся равенством

(4.18 )

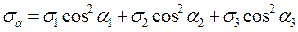
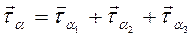
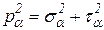
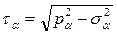
Для вывода формулы касательных напряжений τ_α следует рассмотреть его векторную величину . Так как , то .

Опуская выводы, которые следуют из уравнений равновесия рассматриваемой трёх- гранной пирамиды (рис. 3.11), запишем формулу в окончательном виде для вектора полного напряжения на площадке n_α :

.

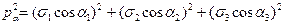
С учётом этого выражения

(4.19)

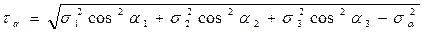
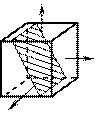
В качестве примера рассмотрим напряжения на площадке, равнонаклонённой ко всем главным площадкам. Такая площадка называется октаэдрической, а напряжения, действующие на этой площадке, называются октаэдрическими.

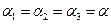
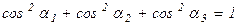
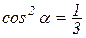
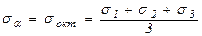
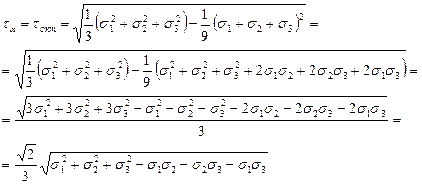
Так как для такой площадки , а учитывая, что всегда

, то . Следовательно (4.20)

(4.21)

Так же, как и в случае плоского напряженного состояния, при объемном напряженном состоянии сумма нормальных напряжений по трем взаимно перпендикулярным площадкам, проходящим через рассматриваемую точку, есть величина постоянная.

Рассмотрим графический метод анализа напряженного состояния в точке при объемном напряженном состоянии.

Прежде всего определим напряжения на площадках, параллельных одному из главных напряжений (рис. 4.12)

s2

s1

s3

На площадках, параллельных s₁, (рис. 4.12, а), напряжения зависят только от s₂ и s₃ и не зависят от s₁, т. к. 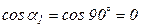, тогда согласно (4.18)

Круг Мора, соответствующий этому случаю, представлен на рис. 4.13 кругом «а».

Напряжения в семействе площадок, параллельных s₂ , определяются по кругу «б», а в семействе площадок, параллельных s₃ – с помощью круга «в».

В теории упругости доказывается, что площадкам общего положения соответствуют точки, лежащие в заштрихованной области (рис. 4.13).

Из представленного рисунка следует, что наименьшее и наибольшее нормальные напряжения равны наименьшему и наибольшему главным напряжениям , .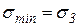

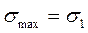
Наибольшие касательные напряжения равны радиусу наибольшего круга

и действуют по площадке, равнонаклонённой к площадкам максимального и минимального из главных напряжений ().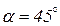

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник