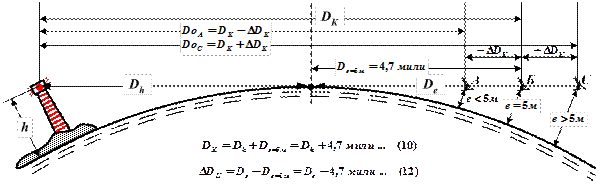Видимый горизонт и дальность видимости
Расчет видимого горизонта и дальности видимости в зависимости от высоты наблюдателя и наблюдаемого объекта.
Калькулятор ниже предназначен для расчета видимого горизонта и дальности видимости в зависимости от высоты наблюдателя и наблюдаемого объекта. Под ним, как водится, немного теории.
Видимый горизонт и дальность видимости
Видимый горизонт
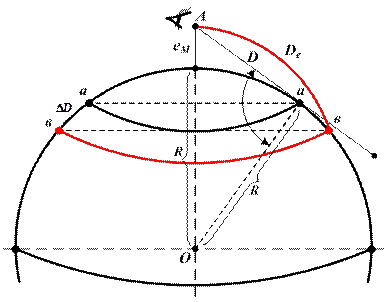
Так как земля изогнута, наблюдателю, находящемуся, например, в море, представляется, что он находится в центре круга, по краям которого небо как бы смыкается с морской поверхностью. Эта окружность и называется видимым горизонтом наблюдателя. На картинке слева видимый горизонт обозначен пунктирной линией. То есть для наблюдателя, находящегося в точке А на высоте h от земли, видимый горизонт будет образован всеми точками касания лучей зрения земной поверхности (угол BCO равен 90 градусов).
Говоря о видимом горизонте чаще всего имеют в виду длину d отрезка BC. Длину d легко вывести из теоремы Пифагора.
где R — радиус Земли, который обычно принимают за 6378 километров.
В реальной жизни на стороне человека выступает атмосфера. Она, благодаря явлению рефракции, то есть преломлению лучей в верхних слоях атмосферы, расширяет его горизонты примерно на 6% 🙂
Формула, таким образом, принимает вид
В принципе, везде (по крайней мере, насколько я находил в Интернете) для расчетов используют упрощенную формулу, из которой исключен радиус Земли. Она, кстати, вполне выводится из верхней.
, для результата в морских милях или
, для результата в километрах
Дальность видимости
Дальность видимости предметов определяется наибольшим расстоянием, на котором наблюдатель увидит вершину наблюдаемого объекта на линии горизонта. Как видно из рисунка, она зависит как от высоты наблюдателя, так и от высоты наблюдаемого объекта. Собственно, это сумма дальности видимого горизонта наблюдателя и дальности видимого горизонта наблюдаемого объекта. Это довольно важный параметр для навигации.
В калькуляторе я ее вычисляю, а на практике, насколько я понимаю, дальности видимости береговых ориентиров указываются во всяческих лоциях, мореходных таблицах и тому подобном для высоты наблюдателя, равной пяти метрам. Для поправки на фактическую высоту наблюдателя используется «номограмма для расчета дальности видимости предметов в море в дневное время при среднем состоянии атмосферы».
Источник
ДАЛЬНОСТЬ ВИДИМОСТИ ГОРИЗОНТА И ОРИЕНТИРОВ В МОРЕ
Дальность видимости горизонта
Наблюдаемая в море линия, по которой море как бы соединяется с небосводом, называется видимым горизонтом наблюдателя.
Если глаз наблюдателя находится на высоте еМ над уровнем моря (т. А рис. 2.13), то луч зрения идущий по касательной к земной поверхности, определяет на земной поверхности малый круг аа, радиуса D.
Рис. 2.13. Дальность видимости горизонта
Это было бы верно, если бы Землю не окружала атмосфера.
Если принять Землю за шар и исключить влияние атмосферы то, из прямоугольного треугольника ОАа следует: ОА=R+e

Так как величина 
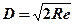
Под действием земной рефракции, в результате преломления зрительного луча в атмосфере, наблюдатель видит горизонт дальше (по кругу вв).
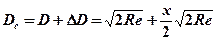
где х – коэффициент земной рефракции (» 0,16).
Если принять дальность видимого горизонта De в милях, а высоту глаза наблюдателя над уровнем моря (еМ) в метрах и подставить значение радиуса Земли (R=3437,7 мили = 6371 км), то окончательно получим формулу для расчета дальности видимого горизонта
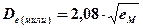
Например:1) е = 4 м Dе = 4,16 мили; 2) е = 9 м Dе = 6,24 мили;
3) е = 16 м Dе = 8,32 мили; 4) е = 25 м Dе = 10,4 мили.
По формуле (2.8) составлена таблица № 22 «МТ-75» (с. 248) и таблица № 2.1 «МТ-2000» (с. 255) по (еМ) от 0,25 м ¸ 5100 м. (см. табл. 2.2)
Дальность видимости ориентиров в море
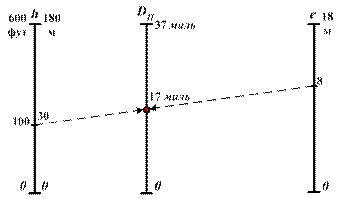
Если наблюдатель, высота глаза которого находится на высоте еМ над уровнем моря (т. А рис. 2.14), наблюдает линию горизонта (т. В) на расстоянии Dе(миль), то, по аналогии, и с ориентира (т. Б), высота которого над уровнем моря hM, видимый горизонт (т. В) наблюдается на расстоянии Dh(миль).
Рис. 2.14. Дальность видимости ориентиров в море
Из рис. 2.14 очевидно, что дальность видимости предмета (ориентира), имеющего высоту над уровнем моря hM, с высоты глаза наблюдателя над уровнем моря еМ будет выражаться формулой:
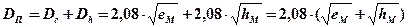
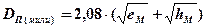
Формула (2.9) решается с помощью таблицы 22 «МТ-75» с. 248 или таблицы 2.3 «МТ-2000» (с. 256).
Решение: для е = 4 м ® Dе = 4,2 мили;
DП = Dе + Dh = 4,2 + 11,4 = 15,6 мили.
Рис. 2.15. Номограмма 2.4. «МТ-2000»
Формулу (2.9) можно решать и с помощью Приложения 6 к «МТ-75» или номограммы 2.4 «МТ-2000» (с. 257) ® рис. 2.15.
Решение: Значения е = 8 м (правая шкала) и h = 30 м (левая шкала) соединяем прямой линией. Точка пересечения этой линии со средней шкалой (DП) и даст нам искомую величину 17,3 миль. (см. табл. 2.3).
Географическая дальность видимости предметов (из табл. 2.3. «МТ-2000»)
Примечание:
Высота навигационного ориентира над уровнем моря выбирается из навигационного руководства для плавания «Огни и знаки» («Огни»).
2.6.3. Дальность видимости огня ориентира, показанная на карте (рис. 2.16)
Рис. 2.16. Дальности видимости огня маяка, показанные
На навигационных морских картах и в навигационных пособиях дальность видимости огня ориентира дана для высоты глаза наблюдателя над уровнем моря е = 5 м, т.е.:

Если же действительная высота глаза наблюдателя над уровнем моря отличается от 5 м, то для определения дальности видимости огня ориентира необходимо к дальности, показанной на карте (в пособии), прибавить (если е > 5 м), или отнять (если е 
— плоскость истинного горизонта наблюдателя (пл. ИГН);
— плоскость истинного меридиана наблюдателя (пл. ИМН);
— плоскость первого вертикала наблюдателя;
— отвесная линия (нормаль) наблюдателя,
— линия истинного меридиана наблюдателя ® полуденная линия N-S;
2. Системами счета направлений являются:
3. Любое направление на поверхности Земли может быть измерено углом в плоскости истинного горизонта, принимая за начало отсчета линию истинного меридиана наблюдателя.
4. Истинные направления (ИК, ИП) определяются на судне относительно северной части истинного меридиана наблюдателя, а КУ (курсовой угол) – относительно носовой части продольной оси судна.
5. Дальность видимого горизонта наблюдателя (De) рассчитывается по формуле:
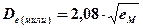
6. Дальность видимости навигационного ориентира (днем в хорошую видимость) рассчитывается по формуле:
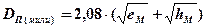
7. Дальность видимости огня навигационного ориентира, по его дальности (DК), показанной на карте, рассчитывается по формуле:


Источник
Сколько километров до горизонта?
Что такое «горизонт»? Мы часто употребляем это слово, например: солнце скрылось за горизонтом или на горизонте показался автомобиль. Но есть ли научное определение данного термина и можно ли измерять расстояние до горизонта?
Что такое горизонт?
Говоря простым языком, это граница между небом и поверхностью земли или воды. Также иногда можно встретить в определении слово «видимый». Горизонт бывает видимым и истинным.
Видимый горизонт – та часть пространства, которую видит наблюдатель, включая границу между небом и земной поверхностью. Истинный горизонт – воображаемый круг небесной сферы, плоскость которого расположена перпендикулярно относительно вертикальной линии в точке наблюдателя. Его также называют астрономическим или математическим.

Расстояние измеряется до видимого горизонта. Для этого используется теорема Пифагора и несложная формула:
Чтобы узнать более-менее точное расстояние, необходимо знать две величины: радиус Земли (R) и высоту, на которой находится наблюдатель (h). Таким образом, очевидно, что чем выше располагается наблюдатель, тем сильнее будет отдаляться линия горизонта.
Примеры расстояния от определенного объекта до горизонта:
- человек ростом 1,75 м, стоящий на земле – 4,7 км;
- крыша 8-этажного дома 25 м – 17,9 км;
- воздушный шар 150 м – 43,8 км;
- самолет 10 км – 357,3 км;
- космический корабль 350 км – 2144 км.
Дальность видимости
Если представить, что наблюдатель стоит на ровной поверхности и ничто не загораживает горизонт, то чем ограничен его кругозор? На открытом пространстве линию горизонта ограничивает выпуклость поверхности Земли, связанная с ее геоидной формой.
Предыдущее изображение показывает, что видимость для наблюдателя заканчивается в той точке, где линия горизонта условно пересекается с геоидной формой Земли. Если наблюдатель поднимется выше, его кругозор расширится.
Возникает вопрос, могут ли различные устройства увеличить дальность видимости? Например, способен ли бинокль расширить кругозор в прямом смысле? Поскольку, бинокль – это оптический прибор, он способен лишь увеличить изображение. Для этого он оснащен специальной конструкцией, которая увеличивает отдаленные объекты, делает их более отчетливыми. Но «заглянуть» за линию горизонта при помощи бинокля нельзя.

Горизонт – граница, разделяющая небо и поверхность земли/воды. Расстояние до видимого горизонта зависит от высоты, на которой находится наблюдатель. Чем выше эта точка, тем сильнее отдаляется горизонт. Например, с высоты среднего человеческого роста (1,75 м) расстояние до горизонта составляет 4,7 км.
Если Вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Источник
Линия горизонт по морю
Если имеется ввиду линия видимого горизонта, то расстояние до неё зависит от высоты расположения глаз наблюдателя. С ходового мостика корабля линия горизонта находится на расстоянии 5 миль.
Если не учитывать преломления воздуха над водой — 4,2 км для человека ростом 1.70. А преломление может быть разным, и увеличивать видимость вплоть до 7 км. Геометрия, 8-й класс; оптика, 9-й класс.
Исчерпывающий ответ, Вы заработали «5» .
Знаете наверное 40км. покрайней мере Америку через пролив Беринга и в ясную погоду не посмотрел. а там до Аляски 72 км.
80 см 3.3 км 200 м 53 км
90 см 3.5 км 250 м 59 км
1.0 м 3.7 км 300 м 64 км
1.1 м 3.9 км 350 м 69 км
1.2 м 4.1 км 400 м 74 км
1.3 м 4.2 км 500 м 83 км
1.4 м 4.4 км 600 м 91 км
1.5 м 4.5 км 700 м 98 км
1.6 м 4.7 км 800 м 110 км
1.7 м 4.8 км 900 м 110 км
1.8 м 5.0 км 1.0 км 120 км
1.9 м 5.1 км 1.5 км 140 км
2.0 м 5.3 км 2.0 км 170 км
2.1 м 5.4 км 2.5 км 190 км
2.2 м 5.5 км 3.0 км 200 км
2.3 м 5.6 км 3.5 км 220 км
2.4 м 5.8 км 4.0 км 230 км
2.5 м 5.9 км 4.5 км 250 км
3.0 м 6.4 км 5.0 км 260 км
3.5 м 6.9 км 6.0 км 290 км
4.0 м 7.4 км 7.0 км 310 км
4.5 м 7.9 км 8.0 км 330 км
5.0 м 8.3 км 9.0 км 350 км
6.0 м 9.1 км 10 км 370 км
7.0 м 9.8 км 11 км 390 км
8.0 м 11 км 12 км 410 км
9.0 м 11 км 13 км 420 км
10 м 12 км 14 км 440 км
11 м 12 км 15 км 460 км
12 м 13 км 20 км 530 км
13 м 13 км 25 км 590 км
14 м 14 км 30 км 640 км
15 м 14 км 35 км 700 км
20 м 17 км 40 км 740 км
25 м 19 км 45 км 790 км
30 м 20 км 50 км 830 км
35 м 22 км 60 км 910 км
40 м 23 км 70 км 990 км
45 м 25 км 80 км 1100 км
50 м 26 км 90 км 1100 км
Спасибо . инструкцию к таблице..если можно
Таблица расстояния до горизонта (удаления горизонта) в зависимости от высоты глаз наблюдателя.
Расстояние до горизонта, конечно, можно вычислить по формуле: S = [(R+h)2 — R2]1/2 где:
S- высота глаз наблюдателя в метрах
R — радиус Земли- обычно: 6367250 м
h — высота глаз наблюдателя над поверхностью в метрах
Но намного удобнее пользоваться таблицей (которая, конечно, приблизительна, да верна только для моря, но все равно — человеку с головой — дает полное представление о явлении):
Высота глаз над
уровнем моря Расстояние до
горизонта Высота глаз над
уровнем моря Расстояние до
горизонта
Спасибо. я редко общался с морем. ну разве что с Морем Лаптева. а вот мой прадед был судовым плотником.. служил на «корейце». поговаривают в ночь перед боем на этом корабле была укорочена мачта. и не один японский снаряд не повредил его. спасибо за таблицу.
Если серьёзно, то линия горизонта /не только морская /. это воображаемая линия! Так что воображайте себе на здоровье!
За линию горизонта можно, принят условную линию, дальше которой не видно продолжение поверхности земли или моря.
№ п/пВысота над поверхностью Земли (моря)
hРасстояние до горизонта
d5.20 м16 км
6.25 м17,9 км
7.30 м19,6 км
8.50 м25,3 км
Источник