Метра над уровнем моря как сокращенно

Высота над уровнем моря — Height above sea level

Высота над средним уровнем моря — это мера вертикального расстояния ( высота , возвышение или высота ) до места по отношению к историческому среднему уровню моря, взятому в качестве вертикальной точки отсчета . Комбинация единицы измерения и физической величины (высоты) в метрической системе называется «метры над средним уровнем моря», в то время как в обычных и имперских единицах США это называется «футы над средним уровнем моря».

На средний уровень моря влияют изменение климата и другие факторы, которые меняются с течением времени. По этой и другим причинам зарегистрированные измерения высоты над уровнем моря в исходный момент истории могут отличаться от фактической высоты данного места над уровнем моря в данный момент.

СОДЕРЖАНИЕ

Использует

Метры над уровнем моря — это стандартное измерение высоты или высоты над уровнем моря:

Как это определяется

Высота или высота в метрах над уровнем моря местоположения, объекта или точки может быть определена несколькими способами. К наиболее распространенным относятся:

Точное измерение среднего исторического уровня моря является сложной задачей. Оседание массива суши (которое происходит естественным образом в некоторых регионах) может создать видимость повышения уровня моря . И наоборот, отметки на суше, которые поднялись из-за геологических процессов, могут указывать на понижение среднего уровня моря.

Другие единицы измерения

Футы над уровнем моря являются наиболее распространенным аналогом метров над уровнем моря в традиционной системе измерения США, сокращенно FAMSL.

Сокращения

Часто используется только аббревиатура MSL, например гора Эверест (8848 м над уровнем моря), или опорная высота полностью опускается, например гора Эверест (8848 м).

Метры над средним уровнем моря обычно обозначают аббревиатурой MAMSL или MAMSL, основанной на сокращении AMSL, означающем «выше среднего уровня моря».

Другие сокращения — это masl и MASL для «метров над уровнем моря».

Источник

Что значит «над уровнем моря». Как считают этот параметр

Любой географический объект определяется тремя параметрами — широтой, долготой и высотой над уровнем моря. Первые два параметра показывают положение на карте, а третий, то есть высота, — положение точки относительно уровня, принятого за ноль — поверхности Мирового океана.

Высота над уровнем моря может быть как положительной, так и отрицательной величиной. Причем, необязательно объект с отрицательным показателем находится на дне океана . Много территорий как в России, так и по всему миру имеют отрицательную высоту над уровнем моря, так как находятся в низменностях. Так Астрахань находится на высоте -20 м над уровнем моря, Баку — -22 м, а Мертвое море в Израиле — на высоте -422 м.

Уровень Мирового океана — не постоянная величина. Со временем уровень океана растет. Да и в один момент времени в разных частях он различается. На это влияют ветры, течения, температура воздуха, приливы и отливы, приток воды из рек. Для того, чтобы поверхность океана могла использоваться в качестве основы для измерения отметок, была разработана концепция “местного среднего уровня моря”. Это означает что страны (или регионы) выбирают свою собственную точку отсчета для высоты объектов.

Балтийская система высот

В России и некоторых бывших странах СССР используется Балтийская система высот . За ноль принимается средний уровень поверхности Балтийского моря.

При этом высота отсчитывается с помощью Кронштадтского футштока — металлической линейки с нулевой отметкой, которая находится на одной из опор Синего моста в Кронштадте. Этот футшток был установлен в начале 18 века для наблюдений за колебаниями уровня воды в Балтийском море. Затем, после нескольких десятилетий, ученые высчитали средний нулевой уровень воды и установили на футштоке медную пластину. От этого уровня и ведется отсчет высот географических объектов в России.

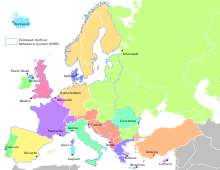
Прочие системы высот В США, Канаде и Мексике принята другая система отсчета высот, в основе которой лежит расчет средних положений для определенных точек. В Великобритании за точку отсчета высоты принимают средний уровень моря, измеренный на юго-западе острова, в гавани Ньюлин. В Турции — уровень воды в Средиземном море в районе Анталии. В Италии и некоторых соседних странах отсчет ведется от положения Евразийской литосферной плиты, а в Нидерландах и Германии — от отсечки, расположенной на Амстердамском футштоке на высоте около 2 м 90 см выше поверхности моря.

Источник

Высота над уровнем моря

Из Википедии — свободной энциклопедии

Высота́ над у́ровнем мо́ря, высота́ — линейная мера разности потенциалов в точке земной поверхности и в начале счёта высот (исходном пункте) [ источник не указан 416 дней ] . В исходном пункте высота принимается равной нулю.

Высота над уровнем моря может быть приблизительно определена как расстояние по вертикали от объекта до среднего уровня поверхности моря, не нарушенного волнением и приливами, или (если объект располагается на суше) до поверхности геоида. Высота точки, лежащей выше уровня моря, считается положительной, ниже — отрицательной.

Разность потенциалов силы тяжести в полной мере характеризует положение двух точек по высоте: вода течёт из точки с меньшим потенциалом в точку с большим потенциалом.

Следует отличать следующие понятия:

• высоту (разность высот) в используемой системе от простой суммы нивелирных превышений: сумма нивелирных превышений зависит от пути, по которому выполнено геометрическое нивелирование.
• высоту (разность высот) в используемой системе от геодезической высоты точки. Геодезическая высота точки — расстояние от точки до поверхности отсчётного земного эллипсоида, она не связана с разностью потенциалов (то есть вода может течь в сторону возрастания геодезической высоты). Геодезическая высота отличается от высоты над уровнем моря на аномалию высоты.

Источник

«Над уровнем моря»: от какого моря считается данный параметр

Получайте на почту один раз в сутки одну самую читаемую статью. Присоединяйтесь к нам в Facebook и ВКонтакте.

В географии существует значение абсолютного нуля, от которого в последствии выполняется измерение высоты (или глубины) географического объекта. Измерения ведутся по шкале от уровня моря. Тем не менее, на планете Земля имеется 63 моря. Учитывая данный факт, многим гражданам наверняка станет интересно, все ли эти водоемы находятся на одном уровне, или какое-то из них все-таки является «эталонным» при расчете высоты и глубины. Здесь все не просто.

Многие забывают о том, что наша планета не выглядит как идеальный шар. А потому и нулевой уровень моря в природе постоянно меняется. Зависит он от огромного числа факторов, среди которых вращение планеты, атмосферное давление и даже конкретные координаты. При выполнении сложных расчетов мореходы и ученые используют усредненный нулевой показатель, который рассчитывается специалистами из показателей регулярных замеров высоты за последние 200 лет.

Кроме того, для упрощения расчётов существует эталонное значение уровня моря. Оно выcчитывается на основании показателей Балтийского моря. Почему именно этого? Здесь все предельно просто. Еще в начале XX века геодезисты установили, что в силу специфики географического положения именно Балтийское море демонстрирует наименьший уровень колебаний по высоте. Суточные и полусуточные амплитуды воды здесь не превышают 20 см, что по сравнению с другими морями на Земле ничтожно мало.

Впрочем, Балтийское море хотя и является самой популярной начальной точкой отсчета, оно не является единственным уловным «абсолютным нулем» в географии.

Если хочется узнать еще больше интересного, то стоит почитать про 14 небанальных карт мира , которые не найти в учебниках по географии.

Понравилась статья? Тогда поддержи нас, жми:

Источник

Высота НУМ

Высота́ над у́ровнем мо́ря, высота́ — линейная мера разности потенциалов в точке земной поверхности и в начале счёта высот (исходном пункте) [ источник не указан 416 дней ] . В исходном пункте высота принимается равной нулю.

Высота над уровнем моря может быть приблизительно определена как расстояние по вертикали от объекта до среднего уровня поверхности моря, не нарушенного волнением и приливами, или (если объект располагается на суше) до поверхности геоида. Высота точки, лежащей выше уровня моря, считается положительной, ниже — отрицательной.

Разность потенциалов силы тяжести в полной мере характеризует положение двух точек по высоте: вода течёт из точки с меньшим потенциалом в точку с большим потенциалом.

Следует отличать следующие понятия:

• высоту (разность высот) в используемой системе от простой суммы нивелирных превышений: сумма нивелирных превышений зависит от пути, по которому выполнено геометрическое нивелирование.
• высоту (разность высот) в используемой системе от геодезической высоты точки. Геодезическая высота точки — расстояние от точки до поверхности отсчётного земного эллипсоида, она не связана с разностью потенциалов (то есть вода может течь в сторону возрастания геодезической высоты). Геодезическая высота отличается от высоты над уровнем моря на аномалию высоты.

Содержание

История понятия

К середине XIX века стало ясно, что при определении высот из геометрического нивелирования нельзя более полагать выводимые превышения равными разностям расстояний от центра Земли — необходимо иметь в виду нецентральность земного гравитационного поля, непараллельность уровенных поверхностей потенциала земной силы тяжести. А. П. Болотов [1] , следуя французскому академику Л. Пюиссану [en] [2] [3] отметил возможность счёта высот по перпендикулярам к сфероидальным поверхностям, параллельным поверхности океана. Л. Пюиссан [en] в книге 1805 года описал принципы геометрического нивелирования, не использовав сам термин «нивелирование» (сс. 230—237), но имея в виду поправки за рефракцию по Лапласу (сс. 223—229). Разности высот считал равными разностям расстояний до центра сферической Земли. Термин «нивелирование» появился в книге Пюиссана 1807 г. [4] Лаплас [5] дал описание астрономической и земной рефракции и измерение высоты барометром.

Внимание геодезистов к этому кругу вопросов привлекла в 1870 году невязка примерно в 1,2 м полигона геометрического нивелирования, пересёкшего Альпы у Симплона и Сен-Готарда. Позднее выяснилось, что эта невязка — результат просчёта, и влияние силы тяжести в подобных случаях едва ли будет больше дециметра. Теодор Ванд [6] , Г. Захарие (G. Zachariae), Ф. Р. Гельмерт опубликовали свои работы о счёте высот в земном гравитационном поле в этот период. Вклад выдающегося немецкого геодезиста Гельмерта [7] (и последующие публикации) особенно значителен. Именно он правильно оценил упомянутое влияние, им предложены динамические высоты, до сих пор сохранившие свою роль в теории и практике нивелирования (термин появился позднее) и метод вычисления ортометрических высот, служивший в СССР до замены таких высот нормальными. Разрабатывая теорию ортометрических высот — высот над геоидом Гаусса-Листинга, Гельмерт отметил принципиальную невозможность точного их определения по результатам измерений на земной поверхности.

В 1945 году М. С. Молоденский (ЦНИИГАиК) впервые использовал нормальные высоты для решения задачи совместного определения фигуры Земли и внешнего гравитационного поля [8] . Дальнейшее развитие система нормальных высот получила в работах канд. техн. наук В. Ф. Еремеева (ЦНИИГАиК), и окончательно разработана к 1972 г. [9]

Основные системы высот над уровнем моря

1. Динамическая высота (перевод разности потенциалов на линейную меру делением на постоянную величину, близкую к средней силе тяжести, например, среднее значение нормальной силы тяжести на широте 45°). Динамические высоты удобно применять вблизи одной и той же уровенной поверхности замкнутого водоёма или гидротехнического сооружения, в этом случае измеренные превышения не будут отличаться от соответствующей разности динамических высот. Применение динамических высот для решения геодезических задач неудобно, поскольку потребуется вводить поправку за переход к динамическим даже в линии нивелирования низкой точности.
2. Ортометрическая высота (отрезок силовой линии реального поля силы тяжести от геоида Брунса до точки земной поверхности; разность потенциалов переводится в линейную меру делением на среднее интегральное значение реальной силы тяжести вдоль этого отрезка). Приращения ортометрической высоты по вертикали в точности равны приращению длины.
3. Нормальная высота (отрезок силовой линии нормального поля силы тяжести от поверхности уровенного эллипсоида вверх до точки, в которой разность нормального потенциала равна разности реального потенциала; разность потенциалов переводится в линейную меру делением на величину среднего интегрального значения нормальной силы тяжести вдоль этого отрезка). Отметки нормальных высот, хотя и в общем случае непостоянны для одной и той же уровенной поверхности, лучше характеризуют уровенные поверхности с разными потенциалами, чем ортометрические. Приращения нормальной высоты по вертикали не равны приращению длины и соответствуют затуханию аномального гравитационного поля с высотой.
4. Нормально-ортометрическая высота (отрезок силовой линии нормального поля силы тяжести от земной поверхности вниз до точки, в которой разность нормального потенциала равна разности реального потенциала; разность потенциалов переводится в линейную меру делением на величину среднего интегрального значения нормальной силы тяжести вдоль этого отрезка).

Исходный пункт счёта высот

В разных странах используются различные исходные пункты счёта высот.

В России в качестве государственной системы высот используется Балтийская система нормальных высот 1977 года, определённая по результатам уравнивания измерений на пунктах государственной нивелирной сети I и II классов главной высотной основы, выполненного ГУГК СССР в 1977 году. В России и в Казахстане высоты точек земной поверхности над уровнем моря отсчитывают от среднемноголетнего уровня Балтийского моря, зафиксированного отметкой на Кронштадтском футштоке. В разных странах используются различные исходные пункты счёта высот.

Примеры

• Самая высокая точка суши в мире — гора Джомолунгма в Гималаях: 8848 м над уровнем моря [10][11] .
• Самый низкий участок суши в мире — побережье Мёртвого моря: 417,5 м ниже уровня моря.

Высоты горных вершин над уровнем моря определены наклонным визирным лучом из тригонометрическим нивелированием с точностью около 1 м, тогда как геодезическая высота вершины над отсчётным эллипсоидом может быть определена с точностью до 1 см с помощью геодезических ГНСС-приёмников.

Источник