Расчеты грунтов по модели Кулона-Мора
Критерий прочности Мора-Кулона.
В качестве критерия прочности для оползней скольжения (как в скальных так и в дисперсных грунтах) наиболее часто используется зависимость Мора-Кулона:
где τ — прочность на сдвиг; u – поровое давление; σ – эффективное нормальные напряжения; φ’ – эффективный угол внутреннего трения; с – сцепление.
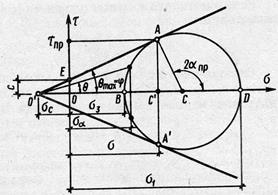
Графическое представление зависимости Мора-Кулона приведено на рис. 1.
Рис. 1. Графическое представление зависимости Мора-Кулона
Условие Мора-кулона может быть использовано как в полных, так и в эффективных напряжениях. В терминах полных напряжений, критерий Мора-кулона приобретает следующую простую форму:
где t — прочность на сдвиг; s – полное нормальные напряжения; j – угол внутреннего трения; с – сцепление.
Необходимыми свойствами грунтов для расчета устойчивости склона на основе критерия прочности Мора-Кулона являются сцепление и угол внутреннего трения. Они не используются в решении, при расчете напряжений и деформаций, но необходимы для расчета зон пластического течения, в которых значения напряжений превысили критические значения и закон Гука не выполняется. Использование критерия прочности Мора-Кулона позволяет сравнить расчетное напряжение при сдвиге с теоретическими предельными значениями напряжений.
Однако, при решении практических задач, перечень необходимых свойств грунтов для оценки устойчивости склонов, существенно расширяется. В зависимости от постановки задачи в полных или эффективных напряжениях, определение прочностных характеристик грунта должно выполняться по недренируемой схеме, или по схеме консолидируемых дренированных испытаний. При оценки устойчивости оползневых склонов (в условиях протекания оползневого процесса) в зоне скольжения должны использоваться остаточные параметры прочности грунтов, при оценке потенциальной оползневой опасности склона (в случае отсутствия оползневого процесса на исследуемом склоне) – должны использоваться пиковые параметры прочности грунтов.
В свою очередь, удельное сцепление грунтов может быть представлено как сумма двух параметров — сс- структурного сцепления и Σw – связанности грунта при заданной влажности.
По Н.Н. Маслову выделяются три типа глинистых грунтов: жёсткие (хрупко-упругие); скрытопластичные (вязкопластичные) и пластичные (вязкотекучие).
К жёстким глинистым грунтам в большинстве случаев относятся грунты до четвертичного возраста. Связанность жестких глинистых грунтов много меньше их структурного сцепления и может быть приравненной к 0, а угол внутреннего трения мало зависит от влажности. Уравнение сопротивления сдвигу для таких грунтов имеет следующий вид:
Прочность на сдвиг скрыто пластичных глинистых грунтов выражается зависимостью:
При этом величины φw и Sw сильно зависят от влажности. В случае нарушения структуры скрытопластичных глинистых грунтов зависимость прочности на сдвиг принимает следующий вид:
Прочность на сдвиг идеально пластичных глинистых грунтов выражается зависимостью:
Как следует из приведенной формулы, в таких грунтах угол внутреннего трения и структурное сцепление принимаются равными 0. В случае нарушения структуры пластичных глинистых грунтов сопротивление прочности на сдвиг в них меняется очень слабо по сравнению с ненарушенной структурой.
В настоящее время существует большое количество модификаций классической зависимости Мора-Кулона. Типичным примером является билинейная модель прочности.
На рис. 1 представлен модифицированный билинейный критерий Мора-Кулона. Огибающая кривая прочности определяется двумя значениями σ (угла внутреннего трения) и удельного сцепления, а также нормальным напряжением в плоскости сдвига, при котором наступает состояние текучести.
Рис. 1. Билинейная модель огибающей кривой сдвига.
Согласно данной модели, в том случае, если нормальное напряжение в плоскости сдвига больше заданного значения, в критерии прочности Мора-Кулона используются значения угла внутреннего трения и сцепления Phi2 и С(computed) соответственно. Билинейная модель прочности была первой попыткой учесть нелинейность в критерии Мора-Кулона.
Типичным примером билинейной модели прочности Мора-Кулона является критерий Паттона (Patton FD (1966). Multiple modes of shear failure in rock. Proceedings of 1st Congress of International Society of Rock Mechanics, Lisbon, 1, 509–513.), разработанный для скальных грунтов и учитывающий эффект шероховатости трещин:
Где φb – базовый угол внутреннего трения породы, i – угол шероховатости, σn – эффективное напряжение, σny — эффективное нормальное напряжение, вызывающее проскальзывание микродефектов шероховатости, сjed – эквивалентное сцепление (прочность на сдвиг за счет зацепления микродефектов).
Данная разновидность модели прочности Мора-Кулона, в последние годы так же нашла широкое применение при оценке устойчивости различных нестационарных состояний оползневых (потенциально оползнеопасных) склонов, таких как падение Ку при быстрой сработке уровня подземных вод или при по этапном псевдостатическом анализе учета сейсмического воздействия (Дункан и Райт).
Модель Кулона-Мора пожалуй самая распространенная модель используемая в геотехнических расчетах. С момента создания данной функции прошло уже несколько столетий, при этом модель не только не потеряла своей актуальности, но и постоянно используется в создании новых аналитических выражений. В инженерно-строительной практике данная модель внедренна в различные методики. С ее помощью рассчитывают основания и фундаменты по двум предельным состояниям.
Источник
Графическая интерпретация теории Кулона-Мора. Условие предельного равновесия.
Приведённые выше положения наглядно иллюстрируются с помощью графического построения кругов напряжений Мора для предельного состояния. Пусть некоторый образец связного грунта испытывался в условиях плоской задачи (рис. 3.17.б) при постоянном значении минимального главного напряжения 
так, чтобы при некотором значении максимального главного напряжения σ1 наступило его разрушение, т. е. в нём сформировались площадки скольжения. В координатных осях τ-σ построим в соответствии с правилами курса сопротивления материалов круг напряжений Мора (рис. 3.18.).
Рис. 3.18. Круг напряжений и график сопротивления сдвигу связного грунта в условиях плоской задачи.
Отложим на оси τ отрезок ОЕ, соответствующий сцеплению с данного грунта. Если теперь через точку Е провести касательную к кругу напряжений, пересекающуюся с осью σ, то получим графическое изображение прямой, соответствующей уравнению сопротивления сдвигу связного грунта (3.40).
Действительно, из треугольника O’AC’ можно записать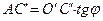 
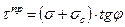
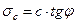
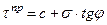
, т. е. 
, что соответствует уравнению (3.43). Поскольку в соответствии с построениями на рис. 3.18. 
, отсюда легко получить зависимость
. (3.40)
Можно также показать, что для любой точки на круге напряжений с координатами τα и σα соответствующими напряжениям на наклонной площадке, не находящейся в предельном состоянии, угол отклонения Θ будет всегда меньше максимального угла отклонения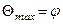 
(см. уравнения (3.46), (3.47)). Также отметим, что прямая сопротивления сдвигу не может пересекать круг напряжений, так как иначе пришлось бы допустить, что Θ может быть больше φ или, что то же самое, τ может быть больше τ пр , а это, как следует из рис. 3.16., физически невозможно.
Точка касания А прямой сопротивления сдвигу к кругу напряжений определяет наклон площадки скольжения к направлению главных напряжений. Поскольку треугольник O’AC прямоугольный, имеем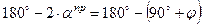 
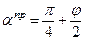
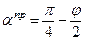
. Отсюда получаем одно из двух условий выражения (3.42): 
. Так как главные напряжения взаимно перпендикулярны, это определяет и второе условие 
. Если же аналогичным образом рассмотреть и вторую касательную к кругу напряжений O’A’ на рис. 3.18., все эти рассуждения можно использовать и для второй сопряжённой площадки скольжения, показанной на рис. 3.17.в.
Из построений на рис. 3.18. легко получить следующее важное условие: так как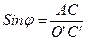 
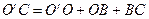
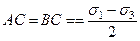
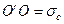
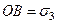
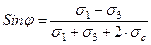
, а 
, то, учитывая, что 
; 
; 
, имеем 
. (3.52)
Выражение (3.52) часто называют условием предельного равновесия связных грунтов, так как оно показывает предельное соотношение между главными напряжениями σ1 и σ3, при котором в данной точке массива грунта, характеризуемого параметрами прочности φ и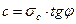 
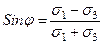
, наступает состояние предельного равновесия. Очевидно, что для сыпучих грунтов, для которых с=0, условие предельного равновесия будет иметь более простой вид
. (3.53)
Отметим, что если в какой-либо точке грунта имеет место такое соотношение главных напряжений, при котором правая часть уравнений (3.52) или (3.53) оказывается меньше величины Sinφ данного грунта, это означает, что грунт в этой точке находится в допредельном состоянии по прочности. В этом нетрудно убедиться, построив соответствующий круг напряжений, так как он не будет касаться прямой сопротивления сдвигу. Соответственно условие, когда правая часть приведённых уравнений оказывается больше величины Sinφ, физически невозможно, поскольку величина Θ не может быть больше φ.
Если учесть, что главные напряжения выражаются через компоненты напряжений с помощью известных зависимостей
, (3.54)
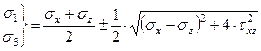
То уравнение (3.52) можно записать в виде
. (3.55)
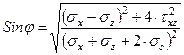
Это условие используется при решении задач теории предельного равновесия. Аналогичным образом выражается уравнение (3.53)
. (3.56)
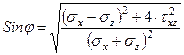
3.4.4. Сопротивление грунта сдвигу при трёхосном сжатии.
Опыты на трёхосное сжатие позволяют испытывать образцы любых грунтов при обжатии их наперёд заданным боковым давлением, что ближе отвечает работе грунта в природных условиях и даёт наиболее надёжные результаты определения их прочностных и деформационных характеристик.
Испытания грунта на трёхосное сжатие обычно проводят в стабилометрах (рис. 3.19).
Рис. 32.19. Схема стабилометра.
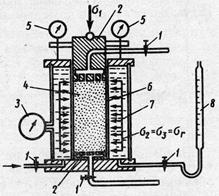
4 – образец грунта;
5 – индикатор часового типа;
6 – резиновая оболочка;
7 – рабочая камера;
Цилиндрический образец грунта (4) помещается в рабочую камеру прибора (7), заполненную водой или глицерином. Для того, чтобы предохранить образец от поступления жидкости, его окружают тонкой резиновой оболочкой (6). Нормальное напряжение σ1 создаётся в образце через штамп (2) с помощью нагрузочного устройства. Боковое напряжение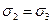 
осуществляется созданием в жидкости рабочей камеры гидростатического давления. Измерение давления в камере производится манометром (3), вертикальных перемещений образца – индикаторами (5). Для отжатия воды из образца в процессе испытания или, наоборот, его насыщения используется система дырчатых штампа и поддона с трубками, прикрытыми кранами (1). Для вычисления горизонтальных перемещений используется тонкая градуированная трубка (волюмометр 8), снабжённая краном (1) и позволяющая определить объём жидкости, вытекающей из рабочей камеры прибора, что соответствует объёмной деформации образца.
Испытания в стабилометре проводятся для изучения деформационных и прочностных характеристик грунтов. Причём в первом случае опыт можно проводить как в условиях компрессионного испытания, так и по схеме трёхосного сжатия. В случае компрессионного испытания кран волюмометра перекрывается, производится вертикальное нагружение образца и с помощью манометра определяются возникающие в результате горизонтальные напряжения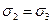 
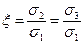
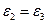
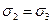
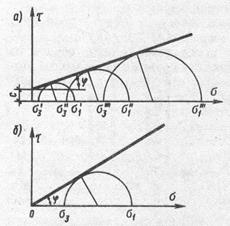
. Это позволяет для любой ступени нагружения по формуле (3.18) вычислить соответствующие значения коэффициента бокового давления 
и коэффициент Пуассона. При испытаниях по схеме трёхосного сжатия кран волюмометра остаётся открытым. По показаниям индикаторов рассчитывают вертикальную деформацию ε1, по уменьшению объёма жидкости в рабочей камере – боковые деформации 
, по показаниям манометра – соответствующие им боковые напряжения и с использованием уравнений (3.26) и (3.27) находят значения модуля объёмного сжатия К и модуля сдвига G.
Прочностные характеристики грунта в стабилометре определяют испытанием нескольких образцов-близнецов. Для этого в каждом испытании к образцу прикладывается постоянное, но разное для различных образцов боковое давление. Для каждого из этих образцов определяется значение σ1, соответствующее разрушению. Затем по результатам испытаний строят круги предельных напряжений (рис. 3.20.). Касательная к этим кругам позволяет определить параметры сопротивления грунта сдвигу φ и с. Для песчаного грунта достаточно проведения одного опыта, так как при с=0 касательная к кругу Мора в этом случае выходит из начала координат (рис. 3.20.а). Уравнения касательных к кругам напряжений для связных и сыпучих грунтов, (3.52) и (3.53), соответственно, выведены ранее.
Рис. 3.20. Определение прочностных характеристик грунта по опытам в стабилометре:
Источник