- Способ вычисления интеграла Мора путем замены непосредственного интегрирования перемножением соответствующих эпюр
- Вычисление интеграла Мора способом Верещагина
- Вычисление интегралов мора по способу верещагина
- Вычисление интегралов мора по способу верещагина
- ПроСопромат.ру
- Технический портал, посвященный Сопромату и истории его создания
- Интеграл Мора
- Метод мора
Способ вычисления интеграла Мора путем замены непосредственного интегрирования перемножением соответствующих эпюр
Вычисление интеграла Мора способом Верещагина
Взятие интеграла Мора не всегда удобно и связано с необходимостью составления функции внутренних сил. Поэтому вместо интегрирования интеграла Мора можно воспользоваться графоаналитическим способом -способом перемножения эпюр (способом Верещагина). Рассмотрим этот метод подробнее.
Рассмотрим две эпюры (рис. 102). Пусть одна имеет произвольное очертание, а другая — прямолинейное.
Пусть жесткость балки на рассматриваемом участке величина постоянная
Отметим, что отношение, вынесенное за знак интеграла, не зависит от координаты z.
Способ Верещагина перемножения эпюр можно сформулировать следующим образом.
Интеграл Мора равен произведению площади эпюры 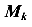
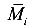
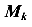
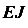
Интеграл (значение) считается положительным, если обе эпюры изгибающих моментов расположены по одну сторону от оси балки. Если перемножаемые эпюры располагаются по разные стороны от оси балки, то значение интеграла, полученное способом Верещагина, принимается отрицательным.
Отметим, что если брать интеграл непосредственно, то знак получается в результате вычислений «как бы автоматически». В способе Верещагина его следует ставить по вышеуказанному правилу.
Положительное значение интеграла означает, что направление перемещения совпадает с направлением единичной силы (или момента).
Способ вычисления интеграла Мора путем замены непосредственного интегрирования перемножением соответствующих эпюр называется способом (или правилом) Верещагина, который предложил студент МИИЖТ Верещагин в 1924.
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Дополнительные страницы которые вам будут полезны:
Изучу , оценю , оплатите , через 2-3 дня всё будет на «4» или «5» !
Откройте сайт на смартфоне, нажмите на кнопку «написать в чат» и чат в whatsapp запустится автоматически.
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Источник
Вычисление интегралов мора по способу верещагина




Вычисление интегралов мора по способу верещагина
- Расчет Интеграла по методу Мора Верещагина Если один из графиков (фактические состояния или единицы измерения) является прямой линией, вычисление интеграла моля значительно упрощается. Это условие, поскольку участок от одной нагрузки (концентрации или пары) всегда ограничен прямой линией, всегда выполняется для
системы, состоящей из прямых стержней. Вычислите Интеграл^M (A4pdx), если график от заданной нагрузки имеет произвольную форму и от единиц измерения — 380-прямая (рис. 377). Представляет площадь участка M g\s-его центроид, MS-вертикальная ось участка от единичной нагрузки под центроидом участка Mr Mpdx=dQ-дифференциальная область участка Mr, L4 Людмила Фирмаль
(13.59)представляет собой статический момент площади участка Mr для оси o-o: XdQ Дж. =х^г, / Где УГ-это абсцисса центра тяжести МР сюжет. В этом случае MtM Pdx = tg ahgy= = YL4G, (13.60) j Я Потому что… Таким образом, Интеграл Мора является свойством участка от внешней нагрузки в ординате линейного участка от единичной нагрузки, расположенной ниже центроида участка от заданной
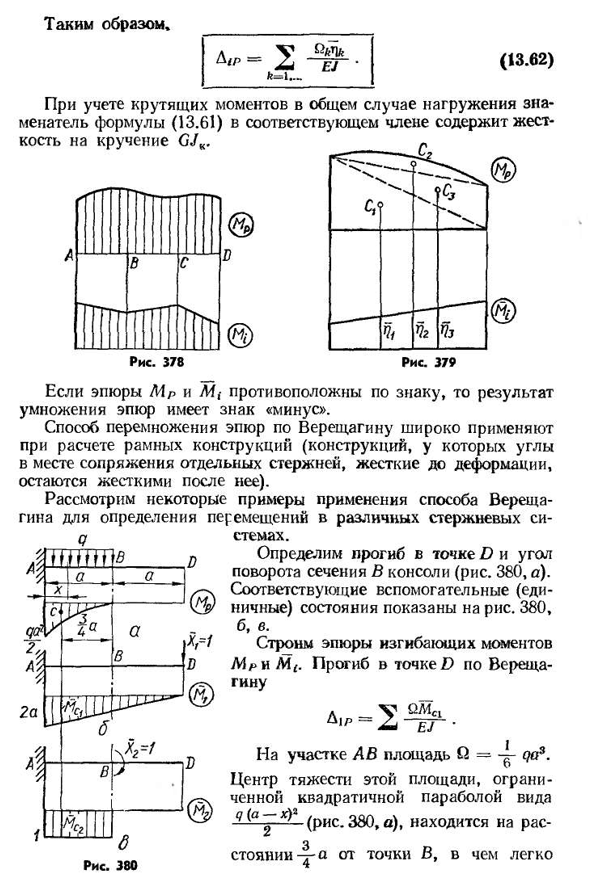
внешней нагрузки. Общая формула перемещения для системы линейных элементов (13.46) имеет вид (13.61) Описывается графоаналитический метод вычисления интеграла Mora. II. It предложен Верещагиным и называется методом Верещагина. Расчет по этой формуле проводится на каждом участке, где участок от единичной загрузки должен быть линейным(рис. 378). Если оба участка прямые, вы можете умножить любую область на ординату
- другой под первым центроидом. Если участок M R имеет сложную форму, то его следует разбить на простые фигуры(рис. 379), ибо легче определить площадь и расположение центра тяжести. В этом случае каждая область умножается на ординату единичного участка, которая находится ниже центроида соответствующей области. В этом случае удобно указать вместо символа MEK G)L, k-1;2;… 3s1 следующим образом* (13.62) Рассматривая крутящий момент в общем случае нагрузки, знаменатель уравнения соответствующего члена (13.61) содержит жесткость на кручение GJ Если участок Mr противоположе
н знаку, то результат умножения участка имеет знак минус. Метод умножения участка Верещагина широко используется при расчете каркасной конструкции (угол на границе раздела отдельных стержней, жесткость до деформации, затем остается жесткой). В данной работе рассматривается применение метода Верещагина для определения перемещений в различных стержневых системах. Определите отклонение точки D и угол поворота сечения в консоли (рис. 380, а). Соответствующее вспомогательное (единичное) состояние показано на рисунке. 380, Б, В. Изгибающий момент в точке D по Верещагину строит диаграмму прогиба m pH m s Площадь участка равна(2=qa3.
Центр тяжести этой области окружен вторичной параболой вида (рис. 380, а) находится Людмила Фирмаль
на расстоянии — ^ — от точки в, в чем легко убедиться, применив формулу (2.3). Вертикальная ось вспомогательного участка L4c1=a. BD Q=0 на сайте. Итак, qa *
EG Для определения угла поворота вспомогательная система загружается одной парой. Очевидно, MS2-1. Следовательно, угол поворота секции л У1 2P-EJ
SEJ • Триста восемьдесят один рис Определим полное перемещение точек из кадра, показанного на рисунке. 381, и, предполагая EJ=const. A = вычислить вертикальное и горизонтальное смещения данной точки для определения полного смещения ПЗС. Для определения вертикального перемещения точки с Рама во вспомогательном состоянии нагружается силой x=1, направленной вертикально(рис. 381, б). Основной сюжет Mr показан на рисунке. 381, g, aux Mi-на фиг. 381, д.,
Расчет производится на сайте: SV site Й, = Т; ; Для управления АВ О2 = МХ\й=/. И так оно и есть., Для определения горизонтального перемещения вспомогательной системы горизонтальная сила x2=1(Рис. 381, в). Участок м2 показан на рисунке. 381, е. 383evidentally SV vertical on the site=0, а AV на сайте Vertical t) 2= » gr., Но __Mh2^2Р»
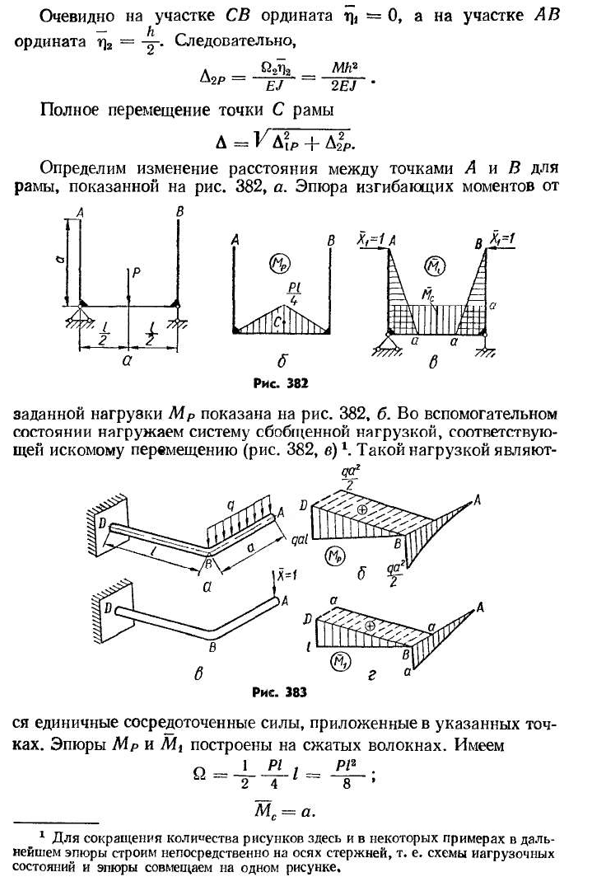
2е Г’ Идеальное смещение пятна от рамки A=D(R+DGR Попробуем определить изменение расстояния между точками кадров, показанных на рисунке. 382, a. график изгиба a и B на мгновение из Данная нагрузка M P показана на рисунке. 382, b.
In вспомогательное состояние, нагружающее систему обобщенной нагрузкой, соответствующей требуемому перемещению (фиг. 382, Б) 1. Такие нагрузки бывают Это единственные силы концентрации, которые действуют в этих точках. Участки Mr и Mi были построены на сжатом волокне. Иметь
8′ _________MS=а. Чтобы уменьшить число фигур 1, в некоторых будущих примерах участок строится непосредственно на оси стержня. 384 противоречия, Но L/R QMC RRA EJ8EJ — Определим падение сломанного консольного свободного конца круглого сечения, нагруженного в сечение АВ вертикальной равномерной распределенной нагрузкой(рис. 383, а).
Диаграммы изгиба и крутящего момента основного и вспомогательного состояний показаны на рисунке. 383, Б, г. График крутящего момента размещен на горизонтальной плоскости, его координаты представлены пунктирной линией.: Лл / ρ=>1Т^3Т г+,-Y1T1?Л г/2; Т2(т+
Изучу , оценю , оплатите , через 2-3 дня всё будет на «4» или «5» !
Откройте сайт на смартфоне, нажмите на кнопку «написать в чат» и чат в whatsapp запустится автоматически.
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Источник
ПроСопромат.ру
Технический портал, посвященный Сопромату и истории его создания
Интеграл Мора
Для решения вопросов жесткости элементов требуется определять перемещения (линейные, угловые). Существуют несколько способов определения перемещений, одним из которых является определение перемещений по интегралу Мора.
Алгоритм вычисления перемещений по интегралу (формуле) Мора:
1. Составляем выражение изгибающего момента MF от действующей нагрузки.
2. Снимаем с балки (рамы, фермы и т.д.) все нагрузки, и в точке, где необходимо определить перемещение, прикладываем единичную силу 


3. Подставляем выражения моментов в интеграл Мора:
где: Δ — перемещение в общем виде, знак Σ распространяется на все участки балки; EI – изгибная жесткость на участке.
Источник
Метод мора
Содержание:
Метод Максвелла — Мора представляет собой универсальный способ для определения линейных и угловых перемещений в любых плоских и пространственных системах.
- Напомним основные этапы использования метода Максвелла -Мора.
При отыскании линейного перемещения к системе, освобожденной от заданных нагрузок, в направлении искомого перемещения (в заданной точке) прикладывается безразмерная единичная сила. Аналогично, при определении углового перемещения в сечении, поворот которого требуется найти, прикладывается пара сил (в плоскости искомого поворота) с моментом, равным безразмерной единице.
Строятся эпюры внутренних силовых факторов от заданной нагрузки и единичных воздействий.
Искомое перемещение определяется из выражения:
правую часть, которого называют интегралами Мора, где: 








Направление единичного воздействия выбирается произвольно. Полученный по формуле (2.1) положительный результат указывает на то, что направление искомого перемещения совпадает с принятым направлением единичного воздействия, либо противоположно принятому направлению, если получен отрицательный результат.
В формуле (2.1) каждый интеграл четко выражает вклад соответствующей деформации в искомое перемещение. Обычно учитываются лишь основные виды деформации. В конструкциях работающих на изгиб учитывается влияние изгибающих моментов, а поперечными силами пренебрегают.
В комбинированных системах, где часть стержней работает на растяжение-сжатие, а часть — на изгиб, учитываются обе эти деформации. В фермах, где каждый стержень работает на растяжение -сжатие в формуле (2.1) остается только первый интеграл.
В случаях, когда ось бруса прямолинейна и жесткость поперечного сечения в пределах отдельных участков постоянна, интегралы
Мора, входящие в выражение (2.1) целесообразно вычислять, используя правило Верещагина или формулу Симпсона.
Возможно вам будут полезны данные страницы:
Пример решения задачи 2.2.
Определить прогиб конца консольной балки (рис. 2.2,а), учитывая лишь деформации, изгиба, жесткость поперечного сечения балки постоянна.
Решение:
Эпюра изгибающих моментов от заданной нагрузки показана на рис.
Построим единичную эпюру, для этой цели, сняв с балки заданную нагрузку, приложим к концу консоли (точка 
вертикально направленную единичную силу 
единичной силы выбирается произвольно , например направим ее вниз, т.е. предполагаем , что точка 
При заданном загружении (рис. 2.2,в), балка имеет один участок 

Подставляя в полученное уравнение прямой координаты начала и конца участка, построим единичную эпюру изгибающих моментов (рис. 2.2, г ).
Для определения прогиба точки 


Перемещение положительно, так как обе сопрягаемые эпюры, лежат по одну сторону от базы ( продольной оси бруса ).
На участке 

Прогиб сечения 
Знак плюс прогиба 
Пример решения задачи 2.3.
Определить угол поворота сечения 
Решение:
Эпюра изгибающих моментов от заданной нагрузки построена ранее в примере, ее вид показан (рис. 2.3, б).
Построим единичную эпюру, для этой цели, сняв с балки заданую нагрузку, приложим в сечении 

Балка имеет три участка. Сопряжение эпюр проведем по участкам. На первом участке (участок 

На втором участке (участок
обе эпюры изгибающих моментов линейны.
Поэтому интеграл Мора на этом участке можно вычислить по формуле трапеций. Применяя ее, найдем:
Полученные выражения отрицательны потому, что знаки ординат «перемножаемых» эпюр 

Получен отрицательный результат потому, что эпюры 


Полученный знак минус указывает на то, что сечение 
Пример решения задачи 3.1.
Для консольной рамы, рис. 3.1,а, определить вертикальное и горизонтальное перемещение точки 

Решение:
Поскольку при определении перемещений в рамах используется интеграл Мора, содержащий изгибающие моменты, построение эпюр 
Построим грузовую эпюру изгибающих моментов, её вид показан на рис. 3.1,6.
Для определения вертикального и горизонтального перемещение точки 


«Перемножим» грузовую и единичные эпюры в пределах длины каждого участка (стержня).

Горизонтальное перемещение точки
Анализируя, полученные выражения, устанавливаем, что точка 
Для определения угла поворота узла 

«Перемножая» грузовую и единичную эпюры, определим угол поворота узла
Сечение поворачивается против хода часовой стрелки.
Пример решения задачи 3.2.
Для шарнирно опертой рамы со стержнями различной жесткости, рис. 3.2,а, определить горизонтальное перемещение точки 
Решение:
Определим опорные реакции от действия заданных нагрузок.
Строим грузовую эпюру изгибающих моментов (рис. 3.2,6).





единичные эпюры изгибающих моментов, см. рис. 3.2,в,г. «Перемножив» эти эпюры с грузовой эпюрой 
Точка 

На странице -> решение задач по сопротивлению материалов (сопромат) собраны решения задач и заданий с решёнными примерами по всем темам сопротивления материалов.
Присылайте задания в любое время дня и ночи в 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназачен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Источник

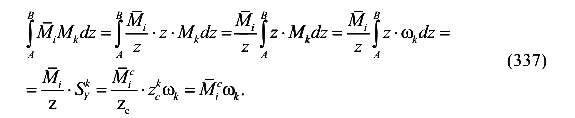
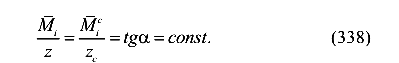
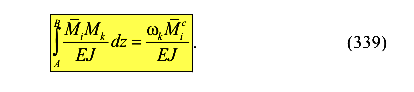













 обе эпюры изгибающих моментов линейны.
обе эпюры изгибающих моментов линейны.












